“If you can’t measure it, you can’t improve it.” – Peter Drucker
先从一个小故事说起。
2012年,一个Bing的工程师想对搜索界面(SERP)上的一些广告位做一些改进,于是他设计了一个简单的实验:仅让部分用户看到了这些改进以测试效果。结果这些改进在短短几个小时内将Bing的收益提高了12%,即当时的年化1亿美金。
不仅仅是Bing — Facebook, Twitter, Google这样的互联网企业对产品都有极高的迭代诉求,每个月要进行的实验不下上百个。
比如Google,在2016年将搜索结果页右侧的8个广告位完全移除,并将首位的3个广告位改为4个;2017年引入Expanded Text Ads,特意将广告标题变成两行;以及2018年将标题和文字描述都各添一行…这些无一不是持续测试的决策。
 (这样的Google你还记得吗?)
(这样的Google你还记得吗?)
可当面对实际操作,我们经常会听到各式各样的主观臆测,诸如,“如果是我,我肯定不会看”,“微信上加的人多,所以微信广告最适合我”等等;亦或是缺少科学依据的“测试”,诸如,“因为我昨天插了广告牌,今天就来了很多单,所以广告牌效果很好”,“我身边朋友都看到了我的广告,所以我的广告做得很值”等等。
大部分的人都不会缺少这样的想法,但是当这些想法被验证之前,任何“结论”都只能是假设(Hypothesis)。而与其将有限的精力和预算浪费在对于不同假设的争论上,不如利用一个专业的系统去验证这些假设 — 即拥有极高性价比并可以进行数据监测的A/B测试上。
A/B测试 4要素
那么如何设计一个科学的A/B测试来确认自己的广告到底有没有成效?
这要看你的测试有没有以下几个元素:
1. 变量
可以是广告内容,确认控制组与对照组,一次只测试一个变量。
举个例子,你想在Facebook上投放单图广告,而你手头有3套文案,3张图片和5种用户兴趣的选择,你会因此产生45种不同版本的广告针对你的测试周期,给预算造成压力,影响你的测试基准。
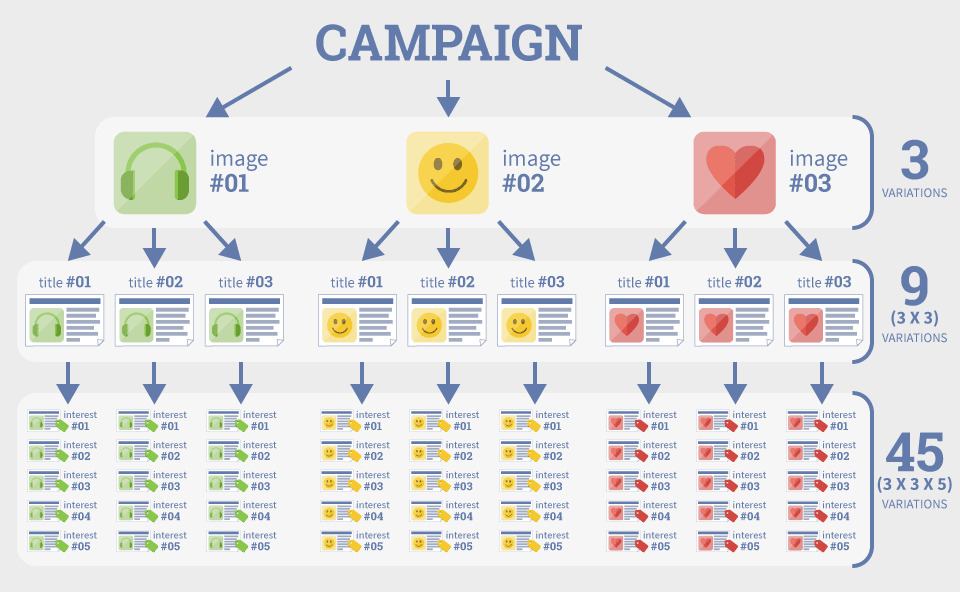
2. 指标
只有确认指标,A/B测试才会有考核标准。这个指标可以是你具体的广告目标, 例如点击率(CTR), 转化率(CVR)等。
3. 周期
理论上是越久越好,但如果样本短时间足够大,则可以选择相对较短的周期来进行A/B测试。但因为受众目标来自不同的行业,所以建议至少应该设立7天的测试周期以照顾到工作日和非工作日的表现。
4. 样本大小
理论上越多越好,但每一个测试组都建议10k次以上曝光。
显著性水平测试
假设我们的广告已经获得足够多的曝光,我们希望能测试两组间的点击量在统计上是否存在明显差异。如果样本量大,我们可以采用z-test(two-sample, one-tailed z-test),如果小,则考虑t-test。
现如今,z-test是当数据在正态分布和随机抽样的假设下运行的,针对对照组A和实验组B进行显著性测试,即null hypothesis零假设(H0)和alternative hypothesis备选假设(Ha)之间有没有显著性差异(significant difference),或者说,所投放的不同广告内容的变化到底有没有影响到点击量。
我们可将样本点击量视为一个正态分布的随机变量,也就是说,样本的点击量是在正态分布下对点击量的一个观测。要了解这一点,请考虑从同一组中提取多个样本进行实验将导致略有不同的点击量。每当对某组进行抽样时,可获得群体点击量的估计,对于A组和B组都是如此。为此我们提出一个新的正态随机变量,它是A组和B组的随机变量的组合,即差值的分布。让我们用X来表示这个新的随机变量,定义为: X=Xe−Xn。
其中,Xe表示实验组的点击量的随机变量,Xn表示对照组的点击量的随机变量。设null hypothesis, H0:X=0, 这表示对照组和实验组是相同的。
两个随机变量Xe和Xn分布在相同的群体平均值周围,所以我们的新随机变量X应该分布在0左右。此时我们将alternative hypothesis设为: Ha:X>0, 实验组的随机变量的期望值大于对照组的期望值;该群体的平均值较高。
我们可以在H0的前提下,对X的分布执行one tail z-test,以确定是否有证据支持alternative hypothesis。为了达到这个目的,我们对X进行样本,计算标准分,并测试已知的显著性水平。
X的样本等效于运行两个实验,确定它们各自的点击量,并将对照组和实验组的点击量相减。按照标准分的定义,可以写作:z=(pexperiment−pcontrol)/SE
其中,pexperiment是实验组的点击量,pcontrol 是对照组的点击量,SE是点击量差值的标准差。
为确定标准误差,注意到点击事件本身是符合二项分布的,因此看到广告可以被看作单次(n=1时)伯努利试验(single Bernoulli trial),且符合伯努利分布。
在样本数量足够大的情况下,我们可以将该分布近似为正态分布进行分析。为了捕获特定点击量的不确定性,我们可以将标准差(SE)写入实验组和对照组,其中p是点击的可能性,n是样本数量:
SE2=p(1-p)/n
从二项分布(np(1-p)的方差得到分子,而分母表示当采用更多的样本时,点击量的误差会随之下降(这也是为什么理论上数据越多越准确!):
SE2=SEexperiment2+SEcontrol2
SEexperiment2=Pexperiment(1-Pexperiment)/Nexperiment
SEcontrol2=Pcontrol(1-Pcontrol)/Ncontrol
将Z引入
z=(Pexperiment-Pcontrol)/(SEexperiment2+SEcontrol2)(½)
z的值越大,反对H0的证据就越多,显著性差异就越大。在设one-tail z-test的90%置信区间(confidence Interval)情况下,z>1.28。这实际上这是指在H0的条件下(A组和B组的人口平均值相同),等于或大于这个点击量差值的偶然发生的概率不到10%。即,在对照组A和实验组B的点击量来自具有相同平均值的分布的假设前提下,如果运行相同的实验1000次,只会有100次具有这样的极端值,因而这个结果是可信的。
*经过简单配置,可以使用在线工具https://abtestguide.com/calc/ 来快速测试显著性
A/B测试在其它领域
A/B测试并不是数字广告领域的专属,事实上可以被运用到很多地方以帮助决策,只是在实验设计中要力求科学。
这里只提一个常见的注意点:幸存者偏差(选择偏差)
简单说就是因为被观察到的特征A造成了结果A1,而忽略了其特征B所造成的结果。举个例子,假设你是一名刚拿到牌的地产经纪,看到的身边朋友在地产公司A混得很不错,在各种活动和媒体上都经常出现,于是你也加入了A公司。
在这个事件中,“在A公司”是被观察到的特征,而结果是”混得不错”,于是你得出了”只要加入A公司就能混得不错”的结论。而同样在A公司的大多数人可能做得都不是很顺,也没有活跃在各路媒体,因而这些人并没有被观察到,且最终对你的决定造成了偏差。
回到实验设计中来。
假设你经营的医美诊所打算在接下来的一周中做个优惠促销,以买一送一的形式,目的是提高他们在未来30天内到店的总回访次数。你对这一周中到访的客户的一半提到了这个优惠(实验组),一半没有提到(对照组),并观察这两波人在未来30天内的回访记录:
| 对比样本 | 总回访次数 |
| 对照组 | 30 |
| 实验组 | 45 |
于是你总结出,做这个优惠会比不做优惠多出50%的门店到访!
可是当我们把选择偏差加进来考虑,不难发现我们在统计中疏漏了实验组中一个子集,即“无论是否有优惠活动都会回访”的高粘客户,因而高估了本次优惠所带来的效益。
这样的偏差在数字广告中一样存在。就像有人总会说“我投不投广告都会有客人,所以投广告没用”,这便是将上述实验中的子集作为唯一的考量所带来的逻辑。
为了解决这一问题,Google特意发明了Ghost Ads(幽灵广告)来缓解现代广告系统中所带来的统计噪音。至于具体细节,我将会在另一篇文章中提到。
如今数字媒体所带来的大量数据最能有效帮助我们更客观,更清晰地判断。倘若可以少一点主观,多一点客观,将这些数据好加利用,一定会为自己的生意增砖添瓦。




